[그래프 ML] 그래프 분해(Graph Factorization) - 파이썬 GEM (Graph Embedding Methods)

※ 출처 : 그래프 머신러닝 (클라우디오 스타밀레 외, 김기성·장기식 옮김)

 

목차

 

---

 

1. 그래프 분해(Graph Factorization)란

1.1. 개념

    행렬 분해를 그래프 데이터, 특히 그래프의 인접 행렬에 적용한 개념입니다. 그래프 분해를 통해 그래프 구조를 저차원의 잠재 공간으로 투영(projection)하는 것을 목표로 합니다. 주어진 그래프 $G$를 작은 차원의 두 행렬 "노드 임베딩 행렬 $F$"와 "잠재 그래프 구조 행렬 $H$"의 곱으로 근사합니다.

$$G \approx F \times H$$

[그래프 ML] 행렬 분해(Matrix Factorization) - 비음수 행렬 분해(NMF), 특이값 분해(SVD), 주성분 분석(PCA)

 

1.2. 활용

    행렬 분해와 마찬가지로 그래프 분해를 통해 그래프의 노드들을 저차원의 잠재 공간에 임베딩할 수 있고, 동시에 그래프의 구조적 패턴을 포착할 수 있습니다.

분야	활용
네트워크 분석	- 통신 네트워크, 소셜 네트워크 구조 분석 - 커뮤니티 구조, 중심성, 연결성 파악
데이터 마이닝 & 패턴 인식	- 대규모 데이터에서 주요 패턴, 구조 발견 - 데이터 클러스터링, 유사성 측정, 이상 탐지
생물 정보학	- 단백질 구조, 유전자 네트워크, 대사 경로 분석 - 생물학적 네트워크의 모듈성, 중요 노드 식별, 기능 예측
웹 마이닝 & 링크 분석	- 웹 페이지와 하이퍼링크 구조를 그래프로 표현하고 분석 - 페이지 랭킹, 커뮤니티 탐색, 권위 페이지 탐색
정보 검색 & 추천 시스템	- 사용자와 아이템 간 관계를 그래프로 표현하고 분석 - 협력 필터링, 관련 아이템 추천, 개별 맞춤화

 

---

 

2. 파이썬 GEM (Graph Embedding Methods) 라이브러리

    그래프 임베딩을 위한 파이썬 라이브러리로, 다양한 알고리즘을 구현하고 있어 효과적으로 그래프 데이터를 임베딩(벡터화) 할 수 있습니다. 임베딩과 관련한 알고리즘 외에도 평가 지표, 데이터 전처리, 시각화 툴을 제공합니다.

※ GEM Paper

GEM: A Python package for graph embedding methods

※ GEM GitHub

GitHub - palash1992/GEM

 

2.1. 설치

pip install git+https://github.com/palash1992/GEM.git

 

2.2. 주요 알고리즘

LLE (Locally Linear Embedding)	지역적으로 선형인 근사를 유지하는 임베딩 기법
Laplacian Eigenmaps	그래프 라플라시안 행렬의 고유벡터를 이용해 투영하는 비선형 임베딩 기법
그래프 분해 (Graph Factorization)
고차원 근접 보존 임베딩 (HOPE; Higher-Order Proximity preserved Embedding)	고유값 분해를 통해 그래프의 구조적 특성을 유지하는 임베딩 기법
SDNE (Structural Deep Network Embedding)	준지도 학습 기반으로 구조 및 특성 정보를 포함하는 임베딩 기법
Node2Vec	노드 시퀀스에 기반한 스킵그램 모델을 활용하는 임베딩 기법

 

2.3. 예제 : 그래프 분해(Graph Factorization)

① 예제 그래프 생성

import networkx as nx

G = nx.barbell_graph(m1=10, m2=4)  # 예제 그래프
nx.draw(G, with_labels=True)  # 그래프 시각화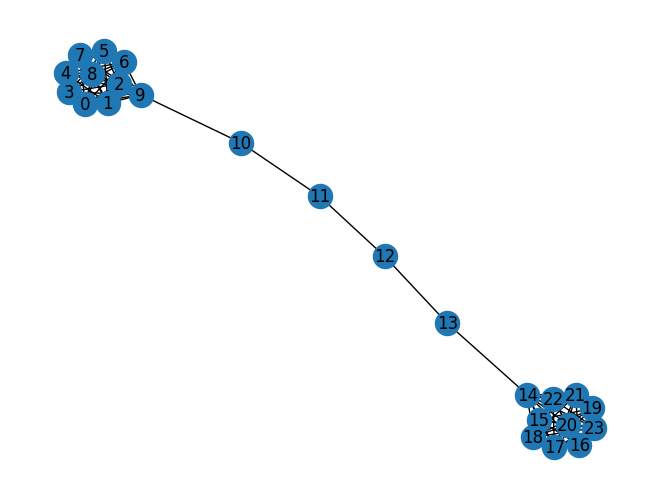

예제 그래프 생성

 

② 그래프 임베딩 학습 및 실행

from gem.embedding.gf import GraphFactorization

gf = GraphFactorization(d=2,  # 임베딩 차원
                        eta=1e-4,  # 확률적 경사 하강법(SGD; Stochastic Gradient Descent)의 학습률
                        regu=0.7,  # 가중치 크기에 대한 정규화 계수
                        max_iter=10000,  # SGD 최대 반복 횟수
                        data_set=None)
# 입력 그래프의 노드 임베딩 연산
gf.learn_embedding(G)
embeddings = gf.get_embedding()
print("그래프 임베딩 크기:", embeddings.shape)

그래프 임베딩 크기: (24, 2)

 

③ 임베딩 결과 시각화

import matplotlib.pyplot as plt

fig, sub = plt.subplots(figsize=(5, 5))
for i, V in enumerate(embeddings):
    v0, v1 = V[0], V[1]
    sub.scatter(v0, v1, s=200)
    sub.annotate(str(i), (v0, v1), fontsize=10, ha="center", va="center")
plt.show()

그래프 분해 결과