[그래프 ML] 그래프 머신러닝 - 파이썬 NetworkX, node2vec, karateclub

목차

• 1. 그래프 머신러닝이란
  • 1.1. 대표적인 그래프 머신러닝 기법
  • 1.2.  그래프 세분화 수준
• 2. 그래프 임베딩 또는 네트워크 임베딩(Graph or Network Embedding)
  • 2.1. 임베딩 알고리즘 분류
• 3. 얕은 임베딩(Shallow Embedding) 예시
  • 3.1. 노드 투 벡터(Node to Vector)
  • 3.2. 엣지 투 벡터(Edge to Vector)
  • 3.3. 그래프 투 벡터(Graph to Vector)

 

※ 출처 : 그래프 머신러닝 (클라우디오 스타밀레 외, 김기성·장기식 옮김)

 

1. 그래프 머신러닝이란

* 그래프 구조로 표현되는 데이터에 대해 기계학습 알고리즘을 적용하는 분야
  - 비정형 구조인 그래프 데이터는 소셜 네트워크, 분자 구조, 지식망, 교통망 등 다양한 영역에서 활용

 

1.1. 대표적인 그래프 머신러닝 기법

* 그래프 임베딩(Graph Embeddings)
* 그래프 신경망(GNN; Graph Neural Network)
* 그래프 커널(Graph Kernels)

→ 노드 분류, 링크 예측, 그래프 생성, 클러스터링 등 작업 수행

 

1.2.  그래프 세분화 수준

수준(Level)	설명	예시
노드 수준 (Node-level)	개별 노드의 특성을 예측하거나 분류	- 소셜 네트워크에서 사용자의 성향 예측 - 분자 구조에서 원자의 종류 예측
간선 수준 (Edge-level)	두 노드 간 연결 고리(링크)가 존재하는지 예측	- 친구 추천 시스템 - 단백질 간 상호작용 예측
서브그래프 수준 (Subgraph-level)	그래프 내 부분 구조를 인식하거나 추출	- 분자 구조에서 특정 기능기 패턴 탐지
그래프 수준 (Graph-level)	전체 그래프의 특성이나 라벨을 예측	- 분자 물성 예측 - 그래프 생성 - 그래프 유사도 계산

그래프 세분화 수준. 출처: Graph Machine Learning with Python Part 1: Basics, Metrics, and Algorithms

 

2. 그래프 임베딩 또는 네트워크 임베딩(Graph or Network Embedding)

* 표현 학습(Representation learning)이라고도 하며, 이산 그래프에서 연속 영역으로 사상 함수(mapping function) $f:G \rightarrow \mathbb{R}^n$를 학습하는 작업
  - 사상 함수 $f$는 그래프 $G$의 속성이 보존되는 저차원 벡터로 표현되도록 동작함

* 사상 함수를 어디에 적용하냐에 따라,
  - $f:G \rightarrow \mathbb{R}^n$ : 그래프 임베딩(Graph embedding)
  - $f:V \rightarrow \mathbb{R}^n$ : 노드 임베딩(Node embedding)
  - $f:E \rightarrow \mathbb{R}^n$ : 간선 임베딩(Edge embedding)

* 임베딩 함수로 생성된 공간에서,
  - 유사한 구조는 유클리드 거리가 짧음
  - 유사하지 않은 구조는 유클리드 거리가 길게 됨

 

2.1. 임베딩 알고리즘 분류

알고리즘	설명	장점	단점	계산 복잡도	구조정보 활용도
얕은 임베딩 (Shallow Embedding)	노드 속성과 구조적 정보를 결합하여 임베딩 벡터를 생성	연산량 적음	구조정보 활용 제한	낮음	낮음
그래프 자동인코딩 (Graph Auto-encoding)	인코더-디코더 활용하여 노드 임베딩과 그래프 복원을 최적화	그래프 구조 포착	과적합 가능	높음	높음
근방 집계 (Neighborhood Aggregation)	근방 노드 임베딩을 반복 집계하여 대상 노드의 임베딩을 생성	구조정보 통합	하이퍼파라미터 최적화 필요	높음	중간
그래프 정규화 (Graph Regularization)	그래프 구조정보를 정규화 항으로 활용하여 임베딩 학습을 안내	구조정보 활용	정규화 강도 설정 까다로움	중간	높음

알고리즘	지도 학습	비지도 학습
얕은 임베딩 (Shallow Embedding)	O	O
그래프 자동인코딩 (Graph Auto-encoding)	-	O
근방 집계 (Neighborhood Aggregation)	O	O
그래프 정규화 (Graph Regularization)	O (준지도 학습 포함)	-

 

3. 얕은 임베딩(Shallow Embedding) 예시

3.1. 노드 투 벡터(Node to Vector)

* node2vec 라이브러리 설치

pip install node2vec

 

* 아래 그림에서 유사한 구조의 노드는 2차원 임베딩 공간에서 서로 가깝고, 구조가 다른 노드와 비교적 멀리 떨어져 있음
  - 두 클리크(0~6번 노드와 11~17번 노드)가 명확히 구별됨

import networkx as nx
from node2vec import Node2Vec
import matplotlib.pyplot as plt
plt.rc("font", family="Malgun Gothic")


G = nx.barbell_graph(m1=7, m2=4)  # 바벨 그래프(Barbell graph) 생성
encoder = Node2Vec(G, dimensions=2).fit(window=10)  # 2차원 노드 임베딩(Node-level embedding) 알고리즘

fig, subs = plt.subplots(ncols=2, figsize=(11, 5))

nx.draw(G, with_labels=True, font_size=10, node_size=200, ax=subs[0])  # 바벨 그래프 시각화
subs[0].set_title("바벨 그래프")

for x in G.nodes():
    name = str(x)
    V = encoder.wv.get_vector(name)
    v0, v1 = V[0], V[1]
    
    subs[1].scatter(v0, v1, s=200)
    subs[1].annotate(name, (v0, v1), fontsize=10, ha="center", va="center")
subs[1].set_title("노드 투 벡터 결과")

plt.show()

 

3.2. 엣지 투 벡터(Edge to Vector)

import networkx as nx
from node2vec import Node2Vec
from node2vec.edges import HadamardEmbedder
import matplotlib.pyplot as plt
plt.rc("font", family="Malgun Gothic")


G = nx.barbell_graph(m1=7, m2=4)  # 바벨 그래프(Barbell graph) 생성
encoder = Node2Vec(G, dimensions=2).fit(window=10)  # 2차원 노드 임베딩(Node-level embedding) 알고리즘
edge_embedding = HadamardEmbedder(keyed_vectors=encoder.wv)

fig, subs = plt.subplots(ncols=2, figsize=(11, 5))

nx.draw(G, with_labels=True, font_size=10, node_size=200, ax=subs[0])  # 바벨 그래프 시각화
subs[0].set_title("바벨 그래프")

for x in G.edges():
    V = edge_embedding[(str(x[0]), str(x[1]))]
    v0, v1 = V[0], V[1]

    subs[1].scatter(v0, v1, s=200)
    subs[1].annotate(str(x), (v0, v1), fontsize=10, ha="center", va="center")
subs[1].set_title("엣지 투 벡터 결과")

plt.show()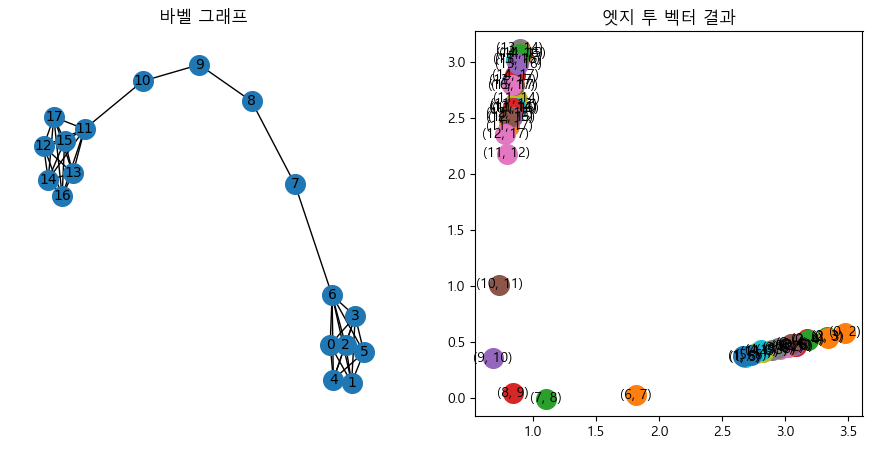

 

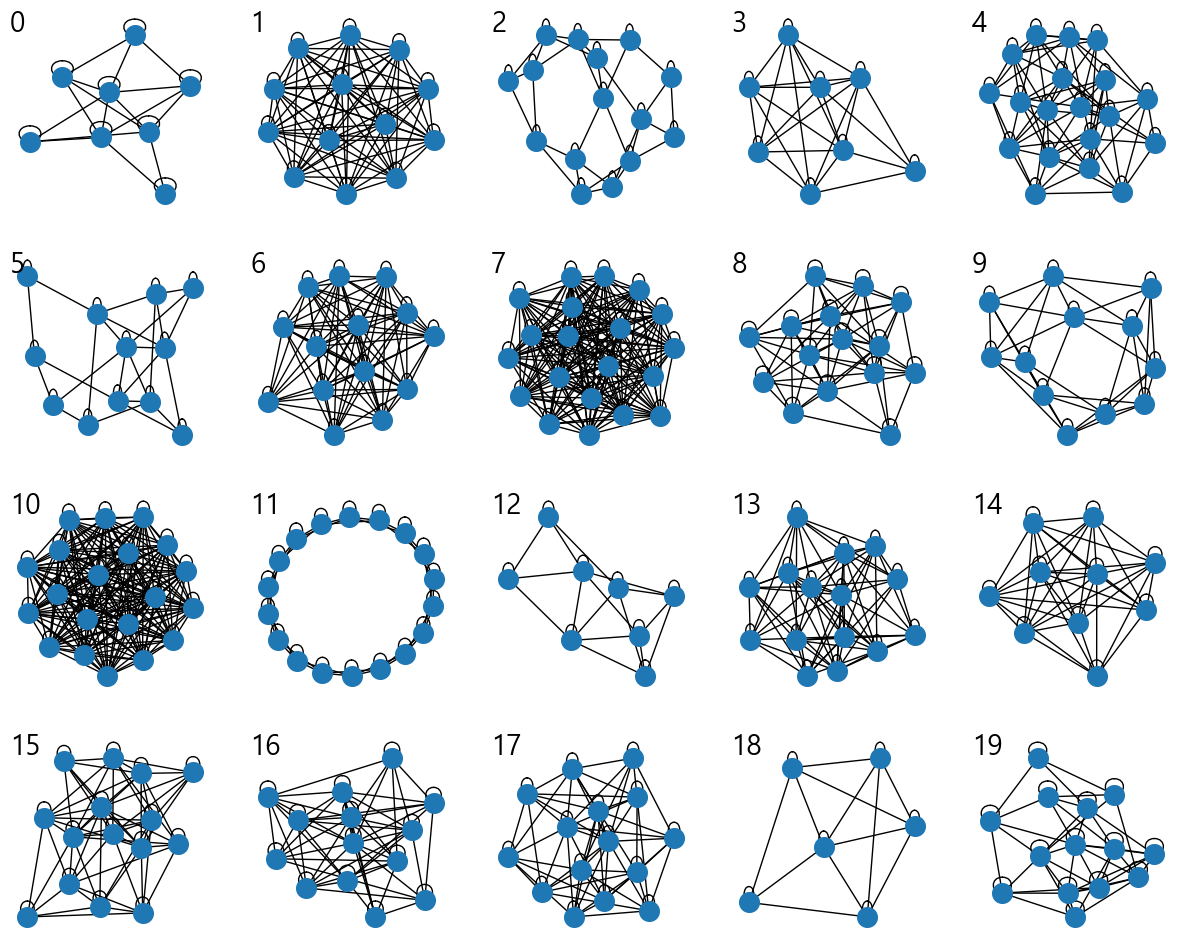
3.3. 그래프 투 벡터(Graph to Vector)

* karateclub 라이브러리 설치

pip install karateclub

 

import random
from karateclub import Graph2Vec
import matplotlib.pyplot as plt
plt.rc("font", family="Malgun Gothic")


def generate_watts_strogatz_graph():  # Watts-Strogatz 그래프 랜덤 생성
    n = random.randint(5, 20)
    k = random.randint(5, n)
    p = random.uniform(0, 1)
    return nx.watts_strogatz_graph(n, k, p)


Gs = [generate_watts_strogatz_graph() for i in range(20)]
encoder = Graph2Vec(dimensions=2)  # 2차원 그래프 임베딩(Graph-level embedding) 알고리즘
encoder.fit(Gs)
graph_embedding = encoder.get_embedding()

fig, subs = plt.subplots(nrows=4, ncols=5, figsize=(15, 12))  # Watts-Strogatz 그래프 시각화
for i, (G, sub) in enumerate(zip(Gs, subs.flatten())):
    nx.draw(G, node_size=200, ax=sub)  # 그래프 시각화
    sub.text(sub.get_xlim()[0], sub.get_ylim()[-1], i, ha="left", va="top", fontsize=20)
plt.show()

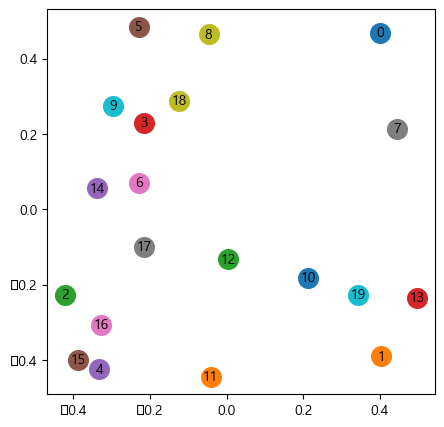
fig, sub = plt.subplots(figsize=(5, 5))  # 그래프 투 벡터 임베딩 결과 시각화
for i, V in enumerate(graph_embedding):
    v0, v1 = V[0], V[1]
    sub.scatter(v0, v1, s=200)
    sub.annotate(str(i), (v0, v1), fontsize=10, ha="center", va="center")
plt.show()