목차
※ 출처 : 그래프 머신러닝 (클라우디오 스타밀레 외, 김기성·장기식 옮김)
※ 이전 글 참고
[그래프 ML] 파이썬 networkx 시작하기
※ 출처 : 그래프 머신러닝 (클라우디오 스타밀레 외, 김기성·장기식 옮김) 1. 그래프(Graph) 뜻 * 개체 간의 관계를 설명하는 데 사용되는 수학적 구조 * 소셜 네트워크(팔로우), 지도(길로 이어진
data-science-note.tistory.com
1. 그래프 속성이란
* 모든 그래프는 고유한 속성을 가지며, 이러한 속성은 측정지표(metrics)로 정량화할 수 있음
- 그래프 전체 / 지역(local) / 전역(global) 측면을 특성화 함
- 간단한 속성 : 노드 및 간선의 개수 → 복잡한 그래프를 표현하기 힘듦
- 통합(Integration), 분리(Segregation), 중심성(Centrality), 탄력성(Resilience) 측정지표를 사용해 그래프의 속성을 보다 잘 표현할 수 있음
| 종류 | 설명 |
| 통합 측정지표(Integration Metrics) | 노드가 상호 연결되는 경향을 측정 |
| 분리 측정지표(Segregation Metrics) | 상호 연결된 노드 그룹의 존재를 측정 |
| 중심성 측정지표(Centrality Metrics) | 개별 노드의 중요성을 측정 |
| 탄력성 측정지표(Resilience Metrics) | 노드 및 간선 추가/제거, 속성 변화 등 변화에 그래프가 얼마나 기능을 유지하는지 측정 |
2. 통합 측정지표(Integration Metrics)
2.1. 거리(Distance), 경로(Path), 최단경로(Shortest Path), 지름(Diameter)
* 거리(Distance)
- 근원 노드(Source node)에서 목표 노드(Target node)에 도달하기 위해 거쳐야 하는 간선의 개수
* 경로(Path)
- 근원 노드와 목표 노드를 연결하는 간선의 집합
* 최단경로(Shortest Path)
- 근원 노드와 목표 노드 사이의 가능한 모든 경로에 대해 간선의 수가 가장 적은 경로
* 지름(Diameter)
- 그래프 내 가능한 모든 최단경로 중 가장 긴 최단경로에 포함된 간선의 수
import networkx as nx
G = nx.Graph()
nodes = {0: "서울", 1: "부산", 2: "인천", 3: "대구", 4: "대전", 5: "광주", 6: "수원"}
G.add_nodes_from(nodes.keys())
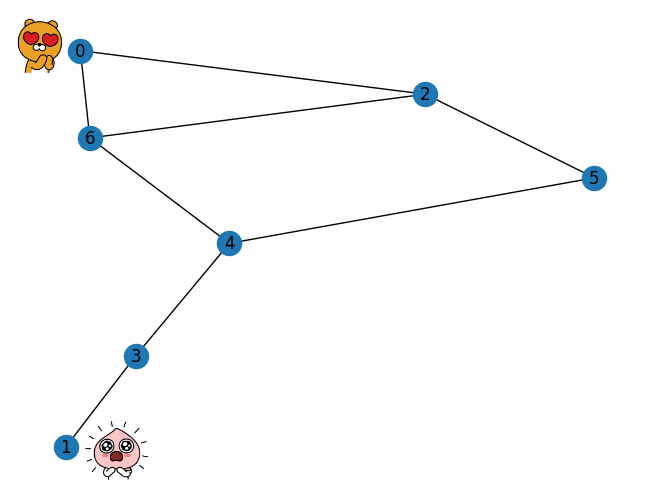
G.add_edges_from([(0, 2), (0, 6), (1, 3), (2, 5), (2, 6), (3, 4), (4, 5), (4, 6)])
shortest_path = nx.shortest_path(G, source=0, target=1) # 0: 서울, 1: 부산
print(f"최단경로: {shortest_path}")
nx.draw(G, with_labels=True) # 그래프 시각화최단경로: [0, 6, 4, 3, 1]
2.2. 특성 경로 길이(Characteristic Path Length)
* 정보가 네트워크를 통해 얼마나 효율적으로 분산되는지 측정하는 방법
- 특성 경로 길이가 짧은 네트워크는 정보를 빠르게 전송할 수 있어 비용 절감에 유리
* 가능한 모든 노드 쌍 사이의 모든 최단경로 길이의 평균
$$\frac{1}{q(q-1)} \sum_{i \in V} l_i$$
- $l_i$ : 노드 $i$와 다른 모든 노드 사이의 평균 경로 길이
- $V$ : 그래프 노드의 집합
- $q = |V|$ : 그래프의 위수
* 문제점 : 연결이 끊긴 그래프에서는 모든 노드 간의 경로를 계산할 수 없기 때문에, 항상 측정할 수는 없음
print(f"특성 경로 길이: {nx.average_shortest_path_length(G)}")특성 경로 길이: 2.0
2.3. 전역 효율성(Global Efficiency)
* 네트워크를 통해 정보가 얼마나 효율적으로 교환되는지에 대한 척도
- 그래프가 완전히 연결됐을 때 효율성 최대, 완전히 연결이 끊긴 그래프는 효율성이 최소
* 모든 노드 쌍에 대한 역최단경로(inverse shortest path) 길이의 평균
- 역최단경로(Inverse shortest path) : 목표 노드에서 다른 모든 노드까지의 최단 거리(일반적인 최단경로와 반대로)
$$\frac{1}{q(q-1)} \sum \frac{1}{l_{ij}}$$
- $l_{ij}$ : 노드 $i$와 $j$ 간의 역최단경로
| 완전 연결 그래프(Fully Connected Graph) | 원형 그래프(Circulant Graph) |
| 각 노드는 다른 노드에서 모두 도달할 수 있으므로, 정보가 네트워크를 통해 빠르게 교환됨 |
각 노드에 도달하기 위해서는 여러 노드를 통과해야 하므로, 효율성이 떨어짐 |
| 전역 효율성 ↑ | 전역 효율성 ↓ |
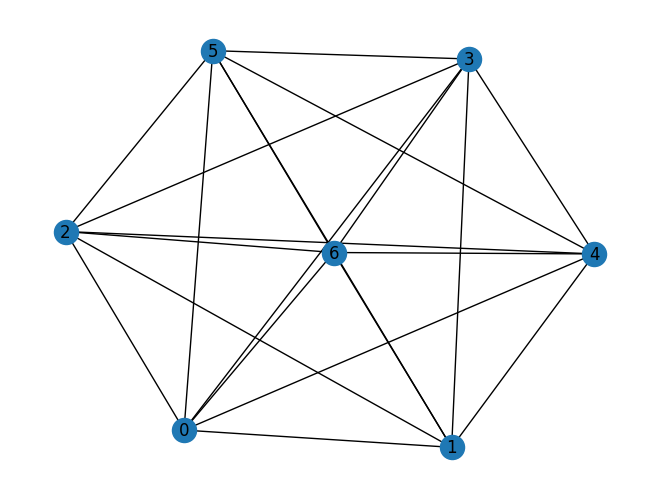
fully_connected_G = nx.complete_graph(7) # 완전 연결 그래프
print(f"완전 연결 그래프의 전역 효율성: {nx.global_efficiency(fully_connected_G)}")
nx.draw(fully_connected_G, with_labels=True) # 그래프 시각화완전 연결 그래프의 전역 효율성: 1.0
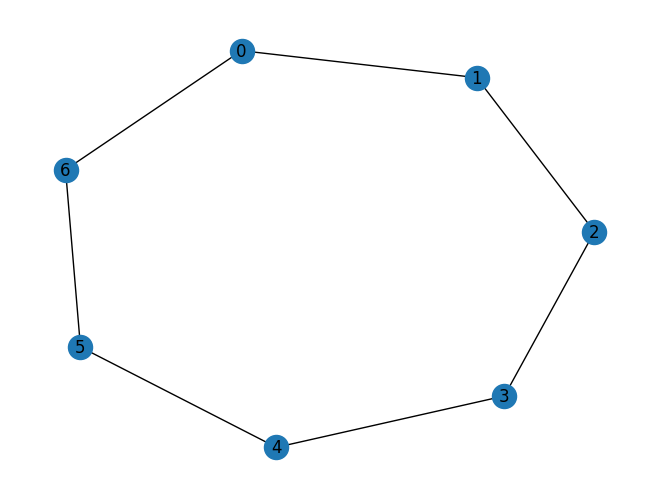
circulant_G = nx.circulant_graph(7, offsets=[1]) # 원형 그래프
print(f"원형 그래프의 전역 효율성: {nx.global_efficiency(circulant_G)}")
nx.draw(circulant_G, with_labels=True) # 그래프 시각화원형 그래프의 전역 효율성: 0.6111111111111109
3. 분리 측정지표(Segregation Metrics)
* 그래프 내 그룹의 존재에 대한 정보
3.1. 군집 계수(Clustering Coefficient)
* 그래프에서 노드들이 서로 얼마나 잘 묶여있는지를 측정하는 지표
* 군집 계수가 높은 경우
- 노드들이 서로 밀집되어 있고 삼각형 구조가 많이 형성됨
- 지역 커뮤니티, 모듈성이 강한 구조를 가진 네트워크
- 생물학에서 기능적으로 연관된 단백질
→ 정보 전파, 전염병 확산이 빠르게 일어날 수 있음
* 군집 계수가 낮은 경우
- 노드들이 분산되어 있고 삼각형 구조가 적음
- 허브 노드를 중심으로 방사형 구조를 가진 네트워크
- 인터넷(www) 같은 복잡한 네트워크
→ 다양한 정보 유입에 유연하게 대처 가능하며, 취약성이 낮음
* 전역 군집 계수(Global Clustering Coefficient)
- 그래프 전체에 대해 계산
- 삼각형(3개 노드와 3개 간선)으로 이뤄진 완전 부분그래프(complete subgraph) 개수를 그래프에 존재할 수 있는 최대 삼각형 개수로 나눈 비율
* 지역 군집 계수(Local Clustering Coefficient)
- 각 노드에 대해 계산
- 한 노드의 이웃 노드들 사이에 연결된 간선 수를 가능한 최대 간선 수로 나눈 비율
G = nx.Graph()
nodes = {0: "서울", 1: "부산", 2: "인천", 3: "대구", 4: "대전", 5: "광주", 6: "수원"}
G.add_nodes_from(nodes.keys())
G.add_edges_from([(0, 2), (0, 6), (1, 3), (2, 5), (2, 6), (3, 4), (4, 5), (4, 6)])
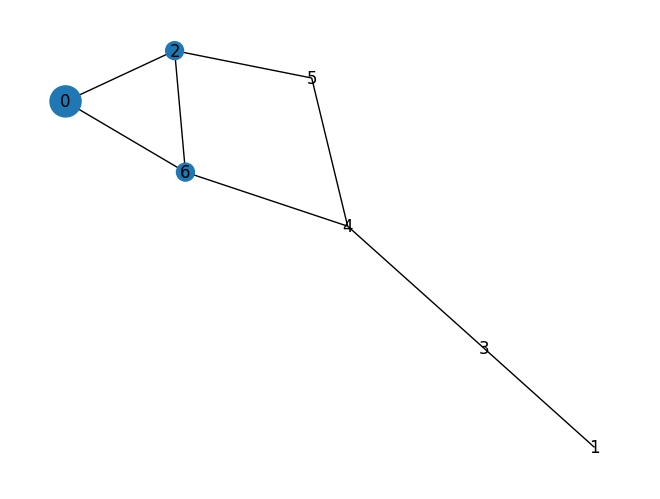
print(f"전역 군집 계수: {nx.average_clustering(G)}")
print(f"지역 군집 계수: {nx.clustering(G)}")
nx.draw(G, with_labels=True, node_size=list(map(lambda x: 500*x, nx.clustering(G).values()))) # 그래프 시각화전역 군집 계수: 0.23809523809523808
지역 군집 계수: {0: 1.0, 1: 0, 2: 0.3333333333333333, 3: 0, 4: 0, 5: 0, 6: 0.3333333333333333}
3.2. 전이성(Transitivity)
* 0과 1 사이의 값을 가지며, 1에 가까울수록 삼각형 구조가 많아 군집화된 구조임을 의미
* 닫힌 트리플렛(Closed triplet; 3개 노드와 2개 간선으로 구성된 완전 부분그래프)의 개수와 그래프에서 가능한 닫힌 트리플렛의 최대 개수의 비율
print(f"전이성: {nx.transitivity(G)}")전이성: 0.25
※ 군집 계수(Clustering Coefficient) vs. 전이성(Transitivity)
| 군집 계수(Clustering Coefficient) | 전이성(Transitivity) | |
| 정의 | 한 노드의 이웃 노드들 사이에 존재하는 간선의 비율 | 전체 그래프에서 연결된 삼각형의 상대적 빈도 |
| 계산 방식 | 개별 노드에 대해 계산 | 그래프 전체에 대해 하나의 값 |
| 범위 | 0 ~ 1 | 0 ~ 1 삼각형이 있어야만 0이 아닌 값을 가짐 |
| 활용 | 개별 노드의 군집화 정도를 파악 | 전체 네트워크의 전역적인 군집화 수준을 파악 |
3.3. 모듈성(Modularity)
* 서로 연결된 노드 집합의 네트워크 분할을 집계하도록 설계됨
- 높은 모듈성을 가진 그래프는 모듈 내에서 밀집된 연결을 보여주고 모듈 간의 연결이 희박함
print(f"모듈성: {nx.algorithms.community.modularity(G, communities=[{0, 2, 6}, {1, 3, 4, 5}])}")모듈성: 0.25
4. 중심성 측정지표(Centrality Metrics)
4.1. 연결 중심성(Degree Centrality)
* 노드의 차수와 특정 노드의 입사 간선(incident edge)의 개수와 연관됨
- 노드가 다른 노드에 많이 연결될수록 해당 노드의 연결 중심성은 높은 값을 가짐
* 유향 그래프라면 들어오는 간선과 나가는 간선의 수와 관련해 각 노드에 대한 내차중심성과 외차중심성을 고려해야 함
print(f"연결 중심성: {nx.degree_centrality(G)}")
연결 중심성: {0: 0.3333333333333333, 1: 0.16666666666666666, 2: 0.5, 3: 0.3333333333333333, 4: 0.5, 5: 0.3333333333333333, 6: 0.5}
4.2. 근접 중심성(Closeness Centrality)
* 노드가 다른 노드와 얼마나 잘 연결되어 있는지를 정량화
* 다른 모든 노드까지의 평균 거리
$$\frac{1}{\sum_{i \in V, i != j} l_{ij}}$$
- $l_{ij}$ : 노드 $i$와 $j$ 간의 최단경로 길이
- $V$ : 노드의 집합
print(f"근접 중심성: {nx.closeness_centrality(G)}")근접 중심성: {0: 0.46153846153846156, 1: 0.35294117647058826, 2: 0.5, 3: 0.5, 4: 0.6666666666666666, 5: 0.5454545454545454, 6: 0.6}
4.3. 매개 중심성(Betweenness Centrality)
* 노드가 다른 노드 간의 다리 역할을 하는 정도
- 해당 노드를 통과하는 최단경로 개수가 많을수록 매개 중심성 값이 높아짐
$$\sum_{w != i != j} \frac{L_{wj}(i)}{L_{wj}}$$
- $L_{wj}$ : 노드 $w$와 $j$ 사이의 최단경로 개수
- $L_{wj}(i)$ : 노드 $i$를 통과하는 $w$와 $j$ 간의 최단경로 개수
print(f"매개 중심성: {nx.betweenness_centrality(G)}")매개 중심성: {0: 0.0, 1: 0.0, 2: 0.1, 3: 0.3333333333333333, 4: 0.5666666666666667, 5: 0.1, 6: 0.3}
※ 중심성 측정지표 비교
import matplotlib.pyplot as plt
plt.rc("font", family="Malgun Gothic")
fig, subs = plt.subplots(ncols=3, figsize=(9, 3))
nx.draw(G, with_labels=True, node_size=list(map(lambda x: 500*x, nx.degree_centrality(G).values())), ax=subs[0]) # 연결 중심성
subs[0].set_title("연결 중심성")
nx.draw(G, with_labels=True, node_size=list(map(lambda x: 500*x, nx.closeness_centrality(G).values())), ax=subs[1]) # 근접 중심성
subs[1].set_title("근접 중심성")
nx.draw(G, with_labels=True, node_size=list(map(lambda x: 500*x, nx.betweenness_centrality(G).values())), ax=subs[2]) # 매개 중심성
subs[2].set_title("매개 중심성")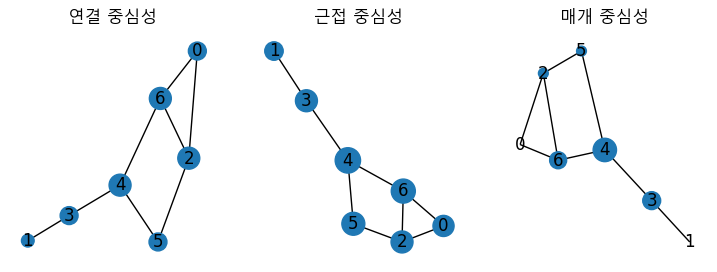
5. 탄력성 측정지표(Resilience Metrics)
5.1. 동류성(Assortativity)
* 그래프에서 연결된 노드들의 유사성 정도를 측정하는 지표로, 특히 노드의 차수가 비슷한 노드들이 서로 연결되어 있는 경향을 파악
* 동류성 계수(Assortativity coefficient)는 -1 ~ 1 사이의 값을 가짐 (∵ 피어슨 상관계수를 사용)
- 양의 계수 : 유사한 차수를 가진 노드들이 서로 연결되는 경향 (동종 연결)
- 0 : 노드 연결에 특별한 경향 없음
- 음의 계수 : 차수가 다른 노드들이 서로 연결되는 경향 (이종 연결)
* 동류성이 높은 경우
- 소셜 네트워크에서 인플루언서끼리 연결되는 경향
- 생태계에서 비슷한 크기의 종들이 상호작용하는 경향
- 이론적으로 동류 네트워크는 노드의 차수 분포가 멱함수 분포를 보이며 견고성이 높음
* 동류성이 낮은 경우
- 핵심 노드(허브)와 주변 노드가 연결된 구조
- 정보 전달이나 확산에 취약
- 이론적으로 노드의 차수 분포가 지수 분포를 보이며 중심성이 높은 노드에 집중됨
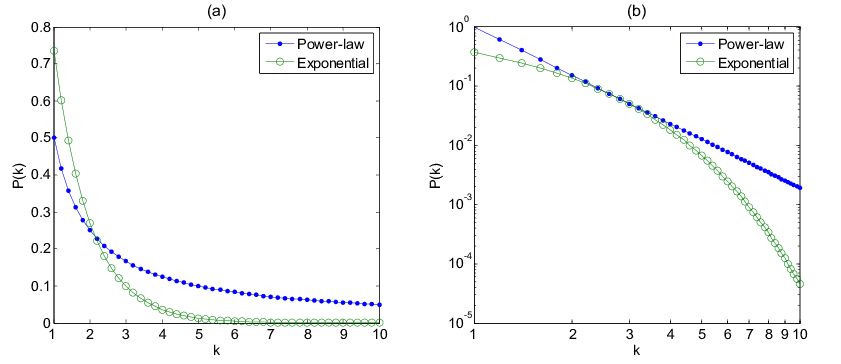
print(f"동류성: {nx.degree_pearson_correlation_coefficient(G)}")동류성: -2.7755575615628914e-17
'인공지능 > 그래프' 카테고리의 다른 글
| [그래프 ML] 에고 그래프 - 파이썬 NetworkX, Gephi (2) | 2024.03.14 |
|---|---|
| [그래프 ML] 그래프 데이터셋 - NetworkX, Network Repository, SNAP (Stanford Network Analysis Platform), OGB (Open Graph Benchmark) (1) | 2024.03.12 |
| [그래프 ML] 그래프 생성 - 파이썬 NetworkX (0) | 2024.03.11 |
| [그래프 ML] Gephi 시작하기 (0) | 2024.03.08 |
| [그래프 ML] 파이썬 NetworkX 시작하기 (1) | 2024.03.08 |
