인공지능/그래프

[그래프 ML] 파이썬 NetworkX 시작하기

백관구 2024. 3. 8. 17:22
반응형

목차

     

    ※ 출처 : 그래프 머신러닝 (클라우디오 스타밀레 외, 김기성·장기식 옮김)

     

    1. 그래프(Graph) 뜻

    * 개체 간의 관계를 설명하는 데 사용되는 수학적 구조
    * 소셜 네트워크(팔로우), 지도(길로 이어진 도시), 생물학적 구조, 웹 페이지, 프로세스 등 여러 분야에 사용됨

     

    2. 라이브러리 설치

    jupyter, networkx, snap-stanford, matplotlib, pandas, scipy

     

    3. 단순무향그래프(Simple Undirected Graph)

    $$G = (V, E)$$

    * $V$ : 꼭지점(vertex) 또는 노드(node)의 집합
    $$V = \{v_1, ..., v_n\}$$

    * $E$ : 두 꼭지점 간의 연결을 나타내는 간선(edge)으로 순서가 없는 순서쌍의 집합
    $$E = \{(v_k, v_w), ..., (v_i, v_j)\}$$
      - 각 간선 간에 순서가 없으므로, $(v_k, v_w), (v_w, v_k)$는 같은 간선을 나타냄

    import networkx as nx

G = nx.Graph()  # 무향그래프
V = {"서울", "부산", "인천", "대구"}  # 문자열, 클래스, 다른 networkx 그래프와 같이 해시가능한 객체
E = [
    ("서울", "부산"),
    ("서울", "인천"),
    ("서울", "대구"),
    ("부산", "대구")
]
G.add_nodes_from(V)
G.add_edges_from(E)

print(f"V = {G.nodes}")
print(f"E = {G.edges}")
    V = ['부산', '서울', '대구', '인천']
    E = [('부산', '서울'), ('부산', '대구'), ('서울', '인천'), ('서울', '대구')]

     

     

    3.1. 기본 속성

    * 그래프 위수(order) $|V|$
      - 노드의 개수

    * 그래프 크기(size) $|E|$
      - 간선의 개수

    * 노드 차수(degree)
      - 해당 노드에 연결된 간선의 개수

    * 노드 근방(neighbor)
      - 노드에 연결된 모든 노드  $V$의 부분집합

    print(f"그래프 위수: {G.number_of_nodes()}")
print(f"그래프 크기: {G.number_of_edges()}")
print(f"노드 차수: { {v: G.degree(v) for v in G.nodes} }")
print(f"노드 근방: { {v: list(G.neighbors(v)) for v in G.nodes} }")
    그래프 위수: 4
    그래프 크기: 4
    노드 차수: {'부산': 2, '서울': 3, '대구': 2, '인천': 1}
    노드 근방: {'부산': ['서울', '대구'], '서울': ['부산', '인천', '대구'], '대구': ['서울', '부산'], '인천': ['서울']}

    * 노드 근방그래프(neighborhood graph) 또는 에고그래프(ego graph)
      - 노드에 연결된 노드와 연결된 모든 변으로 구성된 $G$의 부분그래프(subgraph)

    neighborhood_graph_busan = nx.ego_graph(G, "부산")

print(f"노드: {neighborhood_graph_busan.nodes}")
print(f"간선: {neighborhood_graph_busan.edges}")
    노드: ['부산', '서울', '대구']
    간선: [('부산', '서울'), ('부산', '대구'), ('서울', '대구')]

     

    4. 그래프 종류

    유향그래프(Directed Graph)
    다이그래프(Digraph)    		 가중그래프(Weighted Graph) 다중그래프(Multigraph)

     

    4.1. 유향그래프(Directed Graph)

    $$G = (V, E)$$

    * $V$ : 꼭지점 또는 노드의 집합
    $$V = \{v_1, ..., v_n\}$$
      - 머리(Head) : 출발 노드
      - 꼬리(Tail) : 도착 노드

    * $E$ : 두 꼭지점 간의 연결을 나타내는 간선으로 순서가 있는 순서쌍의 집합
    $$E = \{(v_k, v_w), ..., (v_i, v_j)\}$$
      - 각 간선 간에 순서가 있으므로, $(v_k, v_w), (v_w, v_k)$는 다른 간선을 나타냄
        . $(v_k, v_w)$ : $v_k$ → $v_w$
        . $(v_w, v_k)$ : $v_w$ → $v_k$

    * 노드 차수
      - 입력차수(Indegree) $deg^{-}(v)$ : 노드로 도착하는 간선의 개수
      - 출력차수(Outdegree) $deg^{+}(v)$ : 노드에서 출발하는 간선의 개수

    G = nx.DiGraph()  # 유향그래프
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울"),
    ("인천", "서울"),
    ("대구", "서울"),
    ("부산", "인천"),
    ("대구", "부산"),
    ("대구", "인천")
]
G.add_nodes_from(V)
G.add_edges_from(E)

print(f"입력차수: { {v: G.in_degree(v) for v in G.nodes} }")
print(f"출력차수: { {v: G.out_degree(v) for v in G.nodes} }")
    입력차수: {'부산': 1, '서울': 3, '대구': 0, '인천': 2}
    출력차수: {'부산': 2, '서울': 0, '대구': 3, '인천': 1}

     

    4.2. 다중그래프(Multigraph)

    * 한 노드에서 출발해서 같은 노드로 도착하는 간선이 여러 개인 다중 간선이 있는 그래프

    $$G = (V, E)$$

    * $V$ : 노드의 집합
    * $E$ : 간선의 다중집합
      ※ 다중집합 : 집합의 각 원소에 다중 인스턴스를 허용하는 집합

    * 유향다중그래프(Directed Multigraph)
      - $E$ 순서가 있는 순서쌍의 다중집합
    * 무향다중그래프(Undirected Multigraph)
      - $E$ 순서가 없는 순서쌍의 다중집합

    directed_multi_graph = nx.MultiDiGraph()  # 유향다중그래프
undirected_multi_graph = nx.MultiGraph()  # 무향다중그래프

V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울"),
    ("부산", "서울"),
    ("인천", "서울"),
    ("대구", "서울"),
    ("대구", "서울"),
    ("부산", "인천"),
    ("대구", "부산"),
    ("대구", "인천")
]
directed_multi_graph.add_nodes_from(V)
undirected_multi_graph.add_nodes_from(V)
directed_multi_graph.add_edges_from(E)
undirected_multi_graph.add_edges_from(E)

     

    4.3. 가중그래프(Weighted Graph)

    * 간선가중그래프(Edge-weighted Graph)
      - 일반적인 가중그래프
    $$G = (V, E, w)$$
      - $V$ : 노드의 집합
      - $E$ : 간선의 집합
      - $w:E \to \mathbb{R}$ : 각 간선 $e \in E$를 실수 가중값으로 대응시키는 가중 함수

    * 노드가중그래프(Node-weighted Graph)
    $$G = (V, E, w)$$
      - $V$ : 노드의 집합
      - $E$ : 간선의 집합
      - $w:V \to \mathbb{R}$ : 각 노드 $v \in V$를 실수 가중값으로 대응시키는 가중 함수

    G = nx.DiGraph()
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울", 13),
    ("인천", "서울", 7),
    ("대구", "서울", 10),
    ("부산", "인천", 17),
    ("대구", "부산", 5),
    ("대구", "인천", 15)
]
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

     

    5. 다분그래프(Multipartite Graph)

    5.1. k분그래프(kth-partite Graph)

    * k개의 노드 집합으로 분할할 수 있는 그래프
    * 간선은 서로 다른 집합에 대해서만 허용되며, 같은 집합에 속한 노드 안에서는 허용되지 않음
    * 응용 예시
      - 신용카드 거래 그래프 분석
      - 문서와 그 안의 개체들을 이용한 이분그래프(bipartite graph)로 문서를 처리하고 정보를 구조화

    import pandas as pd
import numpy as np

n_nodes = 10
n_edges = 12

bottom_nodes = [ith for ith in range(n_nodes) if ith%2==0]  # [0, 2, 4, 6, 8]
top_nodes = [ith for ith in range(n_nodes) if ith%2==1]  # [1, 3, 5, 7, 9]
iter_edges = zip(
    np.random.choice(bottom_nodes, n_edges),
    np.random.choice(top_nodes, n_edges)
)
edges = pd.DataFrame([{"source": a, "target": b} for a, b in iter_edges])

B = nx.Graph()
B.add_nodes_from(bottom_nodes, bipartite=0)
B.add_nodes_from(top_nodes, bipartite=1)
B.add_edges_from([tuple(x) for x in edges.values])

from networkx.drawing.layout import bipartite_layout  # 그래프 그리기

pos = bipartite_layout(B, bottom_nodes)
nx.draw_networkx(B, pos=pos)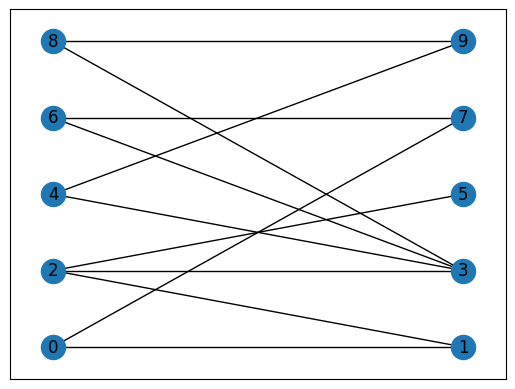

    이분그래프(Bipartite Graph)

     

    6. 인접행렬(Adjacency Matrix)

    * 원소 $M_{ij}$의 값은 노드 $i$에서 노드 $j$로 가는 간선이 있을 때에는 1, 없을 때에는 0인  정방행렬($|V| \times |V|$)

    * 무향그래프
      - 간선의 방향이 없기 때문에 대칭이 됨

    G = nx.Graph()  # 무향그래프
V = {"서울", "부산", "인천", "대구"}  # 문자열, 클래스, 다른 networkx 그래프와 같이 해시가능한 객체
E = [
    ("서울", "부산"),
    ("서울", "인천"),
    ("서울", "대구"),
    ("부산", "대구")
]
G.add_nodes_from(V)
G.add_edges_from(E)

print("Pandas DataFrame:\n", nx.to_pandas_adjacency(G))  # Pandas DataFrame 인접행렬
print("Numpy Array:\n", nx.to_numpy_array(G))  # Numpy Array 인접행렬
    Pandas DataFrame:
            부산 서울 대구 인천
    부산 0.0   1.0   1.0   0.0
    서울 1.0   0.0   1.0   1.0
    대구 1.0   1.0   0.0   0.0
    인천 0.0   1.0   0.0   0.0
    Numpy Array:
    [[0. 1. 1. 0.]
     [1. 0. 1. 1.]
     [1. 1. 0. 0.]
     [0. 1. 0. 0.]]

    * 유향그래프
      - 대칭이 보장되지 않음

    G = nx.DiGraph()  # 유향그래프
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울"),
    ("인천", "서울"),
    ("대구", "서울"),
    ("부산", "인천"),
    ("대구", "부산"),
    ("대구", "인천")
]
G.add_nodes_from(V)
G.add_edges_from(E)

print("Pandas DataFrame:\n", nx.to_pandas_adjacency(G))  # Pandas DataFrame 인접행렬
print("Numpy Array:\n", nx.to_numpy_array(G))  # Numpy Array 인접행렬
    Pandas DataFrame:
            부산 서울 대구 인천
    부산 0.0   1.0   0.0   1.0
    서울 0.0   0.0   0.0   0.0
    대구 1.0   1.0   0.0   1.0
    인천 0.0   1.0   0.0   0.0
    Numpy Array:
    [[0. 1. 0. 1.]
     [0. 0. 0. 0.]
     [1. 1. 0. 1.]
     [0. 1. 0. 0.]]

    * 다중그래프
      - 같은 노드 쌍을 연결하는 간선이 여러 개 있을 수 있으므로, 1보다 큰 값을 가질 수 있음

    G = nx.MultiDiGraph()  # 유향다중그래프
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울"),
    ("부산", "서울"),
    ("인천", "서울"),
    ("대구", "서울"),
    ("대구", "서울"),
    ("부산", "인천"),
    ("대구", "부산"),
    ("대구", "인천")
]
G.add_nodes_from(V)
G.add_edges_from(E)

print("Pandas DataFrame:\n", nx.to_pandas_adjacency(G))  # Pandas DataFrame 인접행렬
print("Numpy Array:\n", nx.to_numpy_array(G))  # Numpy Array 인접행렬
    Pandas DataFrame:
            부산 서울 대구 인천
    부산 0.0   2.0   0.0   1.0
    서울 0.0   0.0   0.0   0.0
    대구 1.0   2.0   0.0   1.0
    인천 0.0   1.0   0.0   0.0
    Numpy Array:
    [[0. 2. 0. 1.]
     [0. 0. 0. 0.]
     [1. 2. 0. 1.]
     [0. 1. 0. 0.]]

    * 가중그래프
      - 인접행렬의 값이 두 노드를 연결하는 간선의 가중값과 같음

    G = nx.DiGraph()
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울", 13),
    ("인천", "서울", 7),
    ("대구", "서울", 10),
    ("부산", "인천", 17),
    ("대구", "부산", 5),
    ("대구", "인천", 15)
]
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

print("Pandas DataFrame:\n", nx.to_pandas_adjacency(G))  # Pandas DataFrame 인접행렬
print("Numpy Array:\n", nx.to_numpy_array(G))  # Numpy Array 인접행렬
    Pandas DataFrame:
            부산 서울 대구 인천
    부산 0.0  13.0  0.0  17.0
    서울 0.0    0.0  0.0    0.0
    대구 5.0  10.0  0.0  15.0
    인천 0.0    7.0  0.0    0.0
    Numpy Array:
    [[ 0. 13. 0. 17.]
     [ 0.   0. 0.   0.]
     [ 5. 10. 0. 15.]
     [ 0.   7. 0.   0.]]

     

    7. 간선 리스트(Edge List)

    * 변 $|E|$의 크기에 대한 리스트
    * 각 원소는 간선이 출발하는 노드와 도착하는 노드의 쌍으로 표현

    G = nx.DiGraph()
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울", 13),
    ("인천", "서울", 7),
    ("대구", "서울", 10),
    ("부산", "인천", 17),
    ("대구", "부산", 5),
    ("대구", "인천", 15)
]
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

print(nx.to_pandas_edgelist(G))
       source target weight
    0 부산    서울   13
    1 부산    인천   17
    2 대구    서울   10
    3 대구    부산     5
    4 대구    인천   15
    5 인천    서울     7

     

    8. 그래프 그리기

    * 노드는 원으로, 간선은 두 노드를 연결하는 선으로 표현

    8.1. NetworkX

    * networkx.draw 함수를 통해 그래프 개체를 그릴 수 있음

    import networkx as nx


def draw_graph(graph, nodes_position: dict, weight):  # nodes_position: {노드 이름: 노드의 위치 좌표(직교좌표계의 2개의 값을 갖는 배열)}
    nx.draw(graph, nodes_position,
            with_labels=True, font_family="Malgun Gothic", font_size=10,  # 각 노드에 이름을 표시
            node_size=400,  # 노드의 크기
            edge_color="grey",  # 간선의 색상
            arrowsize=30)  # 간선의 화살표 크기(유향그래프인 경우)
    if weight:
        edge_labels = nx.get_edge_attributes(graph, "weight")
        nx.draw_networkx_edge_labels(graph, nodes_position, edge_labels=edge_labels)


G = nx.DiGraph()
V = {"서울", "부산", "인천", "대구"}
E = [
    ("부산", "서울", 13),
    ("인천", "서울", 7),
    ("대구", "서울", 10),
    ("부산", "인천", 17),
    ("대구", "부산", 5),
    ("대구", "인천", 15)
]
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

nodes_position = {
    "서울": [1, 1],
    "부산": [1, 0],
    "인천": [0, 1],
    "대구": [0.5, 0]
}
draw_graph(G, nodes_position, True)

    * 노드 레이아웃 종류
      - NetworkX는 레이아웃에 따라 각 노드의 위치를 자동으로 계산하는 기능 지원
      - networkx.drawing.layout 라이브러리에 있는 bipartite_layout, circular_layout, kamada_kawai_layout, planar_layout, random_layout, spring_layout, shell_layout, spectral_layout, spiral_layout 레이아웃 활용 가능
      - 복잡한 그래프는 Gephi를 사용하는 것을 추천!

    import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from networkx.drawing.layout import bipartite_layout, circular_layout, kamada_kawai_layout, planar_layout, random_layout, spring_layout, shell_layout, spectral_layout, spiral_layout


n_nodes = 10
n_edges = 20
nodes = np.arange(n_nodes)  # [0, ..., 9]

fig, subs = plt.subplots(nrows=3, ncols=3, figsize=(9, 9))
for sub, layout in zip(subs.flatten(),
                       [bipartite_layout, circular_layout, kamada_kawai_layout, planar_layout, random_layout, spring_layout, shell_layout, spectral_layout, spiral_layout]):
    iter_edges = zip(
        np.random.choice(nodes[:5], n_edges),
        np.random.choice(nodes[5:], n_edges)
    )
    edges = pd.DataFrame([{"source": a, "target": b} for a, b in iter_edges])
    
    G = nx.Graph()
    G.add_nodes_from(nodes)
    G.add_edges_from([tuple(x) for x in edges.values])
    
    if layout.__name__=="bipartite_layout":
        pos = layout(G, nodes=nodes[:5])
    else:
        pos = layout(G)
    nx.draw(G, pos=pos, ax=sub, with_labels=True, font_size=10, node_size=100)
    sub.set_title(layout.__name__)

    NetworkX 그래프 레이아웃

     

    반응형
    저작자표시 비영리

    '인공지능 > 그래프' 카테고리의 다른 글

    [그래프 ML] 에고 그래프 - 파이썬 NetworkX, Gephi  (2) 2024.03.14
    [그래프 ML] 그래프 데이터셋 - NetworkX, Network Repository, SNAP (Stanford Network Analysis Platform), OGB (Open Graph Benchmark)  (7) 2024.03.12
    [그래프 ML] 그래프 생성 - 파이썬 NetworkX  (0) 2024.03.11
    [그래프 ML] 그래프 속성 - 파이썬 NetworkX  (0) 2024.03.11
    [그래프 ML] Gephi 시작하기  (0) 2024.03.08

    '인공지능/그래프'의 다른글

    • 현재글[그래프 ML] 파이썬 NetworkX 시작하기

    관련글

    댓글

    티스토리툴바