안녕하세요:)

이번 포스팅에서는 OpenCV의 이미지 이진화에 대해 알아보겠습니다.
이진화
이진(Binary) 이미지는 모든 픽셀이 검정과 흰색으로만 표현된 이미지를 가리키며, 이렇게 이미지를 변환하는 과정을 이진화(Binarization)이라고 합니다. 컬러 이미지나 그레이 이미지를 검정과 흰색만 갖고 표현한다고 보시면 됩니다.

위 그림을 예시로 들어보겠습니다. 왼쪽 그림은 원본 컬러 이미지 입니다. 일반적으로 볼 수 있는 빨강(Red), 초록(Green), 파랑(Blue)의 3 채널로 구성되어 있습니다. 빨강, 초록, 파랑의 조합으로 모든 색을 표현하게 됩니다. 각 채널이 0부터 255까지 범위의 값을 갖는다고 하면, 검정색은 빨강 0 / 초록 0 / 파랑 0의 조합으로 만들고 흰색은 빨강 255 / 초록 255 / 파랑 255의 조합으로 만들 수 있습니다.

가운데 그림은 원본 컬러 이미지를 그레이 스케일로 변환한 그레이(Gray) 이미지 입니다. 컬러 이미지의 명암(밝고 어두움)을 표현한 것이 그레이 이미지 입니다. 그레이 이미지는 1 채널로 구성되며, 일반적으로 0부터 255까지의 총 256 단계의 값을 갖습니다. 여기서 256 단계로 나타내게 된 것은 8 비트(2의 8승 = 256)에서 유래한 것으로, 최근에는 정밀한 표현을 위해 16, 32, 64 비트로 표현하기도 합니다. 참고로 64 비트는 2의 64승 단계로 나뉘어 있습니다.
오른쪽 그림이 바로 이진(Binary) 이미지 입니다. 그림을 구성하는 모든 픽셀들이 검정과 흰색으로만 표현된 것이 특징입니다. 그레이 이미지와 마찬가지로 1 채널로 구성됩니다. 그레이 이미지와 다른 점은 특정한 경계값을 기준으로 검정과 흰색의 구분이 뚜렷하다는 점입니다. 식으로 나타내면 아래와 같습니다. 즉 경계값(T)보다 작으면 검정(0)으로, 경계값보다 크면 흰색(255; 8비트의 경우)으로 픽셀의 값을 변환하는 과정이 이진화(Binarization) 입니다.
out(i,j)={255,ifin(i,j)>T0,otherwise
OpenCV 이진화 (cv2.threshold)
OpenCV에서는 cv2.threshold 함수를 사용해서 이진화를 적용합니다. 함수에 입력되는 파라미터와 출력은 아래와 같습니다.
cv2.threshold(src, thresh, maxval, type)
- 입력 이미지를 지정된 경계값(thresh)과 방법(type)을 이용하여 이진화
- Parameters
- src : 이미지 객체 행렬
- thresh : 경계값
- maxval : 출력의 최대값
- type : 이진화 방법 (THRESH_BINARY, THRESH_BINARY_INV, THRESH_TRUNC, THRESH_TOZERO, THRESH_TOZERO_INV)
- Returns : (경계값, 이진 이미지 객체 행렬)
- Return type : float, numpy.ndarray
이진화 방법 (type)
이진화 방법에는 5 가지 종류가 있습니다. 일반적으로 THRESH_BINARY를 주로 사용합니다. 아래 그림을 통해 각 방법의 적용 결과를 확인할 수 있습니다.
1. THRESH_BINARY
일반적인 이진화 방법. 경계값보다 크면 설정한 최대값(maxval)으로, 경계값보다 작으면 0으로 변환
out(i,j)={maxval,ifin(i,j)>thresh0,otherwise
2. THRESH_BINARY_INV
THRESH_BINARY와 반대로 변환. 경계값보다 크면 0으로, 경계값보다 작으면 설정한 최대값(maxval)으로 변환
out(i,j)={0,ifin(i,j)>threshmaxval,otherwise
3. THRESH_TRUNC
경계값보다 크면 설정한 최대값으로 변환, 경계값보다 작으면 기존값 유지
out(i,j)={maxval,ifin(i,j)>threshin(i,j),otherwise
4. THRESH_TOZERO
경계값보다 크면 기존값 유지, 경계값보다 작으면 0으로 변환
out(i,j)={in(i,j),ifin(i,j)>thresh0,otherwise
5. THRESH_TOZERO_INV
THRESH_TOZERO와 반대로 변환. 경계값보다 크면 0으로 변환, 경계값보다 작으면 기존값 유지
out(i,j)={0,ifin(i,j)>threshin(i,j),otherwise

실제 활용 사례를 통해 cv2.threshold의 사용 방법에 대해 알아보겠습니다. 먼저 여기서 사용할 이미지를 가져옵니다. 아래 첨부파일을 받으셔도 되고, 개인적으로 준비하신 파일을 사용하셔도 됩니다.
OpenCV를 이용해 이미지 파일을 이미지 객체 행렬로 불러옵니다. 옵션을 주어 그레이 스케일(cv2.IMREAD_GRAYSCALE)로 읽어오도록 설정하겠습니다.
import cv2 # OpenCV API
sudoku = cv2.imread('./sudoku.jpg', cv2.IMREAD_GRAYSCALE) # 이미지 파일 그레이 스케일로 불러오기
plt.imshow(sudoku, cmap = 'gray') # 이미지 시각화
plt.show()
여기서는 이진화 방법 중 THRESH_BINARY를 활용해 이진 이미지로 변환합니다. 경계값(thresh)을 50, 100, 150으로 줘 이진 이미지의 변화를 보도록 하겠습니다.
bin50 = cv2.threshold(sudoku, 50, 255, cv2.THRESH_BINARY)[1] # thresh = 50 이진화
bin100 = cv2.threshold(sudoku, 100, 255, cv2.THRESH_BINARY)[1] # thresh = 100 이진화
bin150 = cv2.threshold(sudoku, 150, 255, cv2.THRESH_BINARY)[1] # thresh = 150 이진화
fig, subs = plt.subplots(ncols = 3, figsize = (15, 5), sharex = True, sharey = True)
subs[0].set_title('thresh : 50')
subs[0].imshow(bin50, cmap = 'gray')
subs[1].set_title('thresh : 100')
subs[1].imshow(bin100, cmap = 'gray')
subs[2].set_title('thresh : 150')
subs[2].imshow(bin150, cmap = 'gray')
plt.show()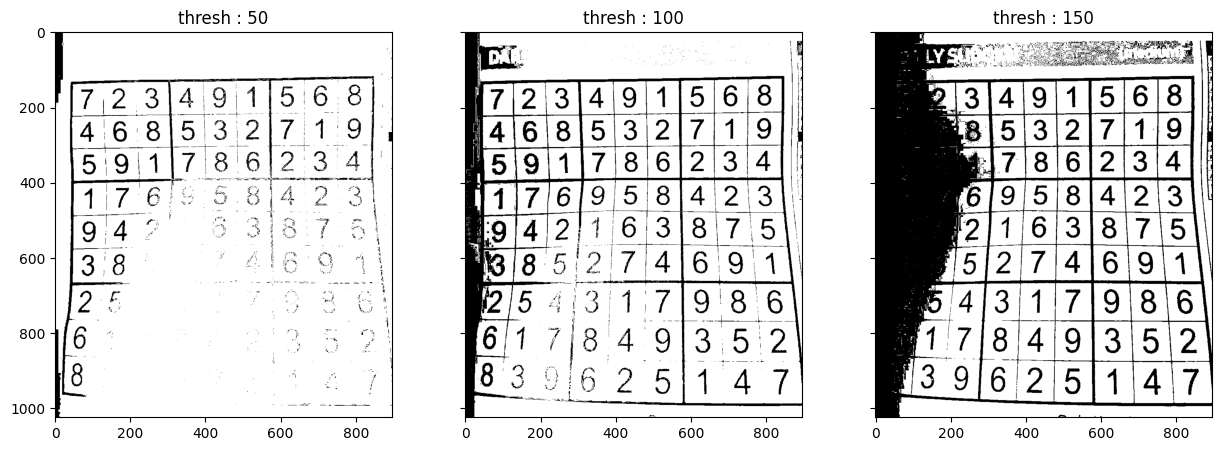
위 사례에서 경계값을 낮게 줬을 때(thresh = 50), 원본 이미지에서 비교적 밝은 아래 부분이 하얗게 표현(최대값으로 변환)되는 것을 확인할 수 있습니다. 더 높은 경계값을 주면(thresh = 100) 보이지 않았던 아래 부분의 숫자들이 보이기 시작하며, thresh = 150으로 경계값을 높게 설정하면 숫자는 또렷하게 보이지만 왼쪽 부분에 있는 그림자 영역의 숫자들을 확인할 수 없게 됩니다.
위 사례처럼 cv2.threshold의 경계값에 따라 이진화의 결과가 크게 달라지는 이유는, 특정 경계값을 이미지 전체에 적용하여 처리하기 때문에 하나의 이미지에서 음영이 다르면 일부 영역이 모두 흰색 또는 검정색으로 보여지게 됩니다. 위 사례의 경우 이미지의 아래 부분은 상대적으로 밝고, 왼쪽 부분은 상대적으로 어둡기 때문에 경계값(thresh)을 무엇으로 설정하느냐에 따라 해당 영역이 모두 흰색 또는 검정색으로 표현됩니다. 이러한 문제점 때문에 적응형 이진화(Adaptive Binarization)를 활용하는 것이 더 바람직합니다.
적응형 이진화 (cv2.adaptiveThreshold)
위와 같은 문제를 해결하기 위해서는 각 픽셀에 대해 적절한 경계값을 기반으로 이진화가 수행되어야 합니다. 그 방법으로 픽셀 주변에 분포하는 값들의 평균을 이용하여 경계값을 설정하는 방법이 있습니다. 이를 식으로 나타내면 아래와 같이 표현합니다. 아래 식에서 h′와 w′는 평균값을 구하기 위해 사용하는 픽셀 주변 블록의 높이와 너비, α는 가중치, C는 조정 상수를 가리킵니다.
T(i,j)=(1h′w′h′−12∑h=−h′−12w′−12∑w=−w′−12αi+w,j+hini+w,j+h)+C
OpenCV는 cv2.adaptiveThreshold 함수를 통해서 적응형 이진화를 지원합니다.
cv2.adaptiveThreshold(src, maxval, adaptiveMethod, thresholdType, blockSize, C)
- 입력 이미지를 설정한 적응 방법(adaptiveMethod)과 블록 크기(blockSize)에 기반하여 이진화
- Parameters
- src : 이미지 객체 행렬
- maxval : 출력의 최대값
- adaptiveMethod : 경계값을 계산하기 위한 적응 방법 (ADAPTIVE_THRESH_MEAN_C, ADAPTIVE_THRESH_GAUSSIAN_C)
- thresholdType : 이진화 방법 (THRESH_BINARY, THRESH_BINARY_INV)
- blockSize : 경계값을 계산하기 위한 블록 크기 (홀수)
- C : 경계값을 조정하기 위한 상수
- Returns : 이진 이미지 객체 행렬
- Return type : numpy.ndarray
적응 방법 (adaptiveMethod)
cv2.adaptiveThreshold의 주요 파라미터인 adaptiveMethod는 경계값을 어떻게 계산할 것인지 설정하며, cv2.ADAPTIVE_THRESH_MEAN_C와 cv2.ADAPTIVE_THRESH_GAUSSIAN_C 중 선택 가능합니다. 이 선택에 따라 위 식의 α (가중치) 값이 다르게 배정됩니다.
ADAPTIVE_THRESH_MEAN_C
α=1 이 되어 경계값을 계산하기 위한 블록 내 값들의 산술평균을 구합니다.
ADAPTIVE_THRESH_GAUSSIAN_C
α 가 가우시안 분포를 따르게 되며, 블록의 중심 픽셀이 가장 큰 비중을 차지하고 블록 가장자리로 갈수록 작은 비중을 차지하는 가중평균을 구합니다.
위에서 사용했던 스도쿠 이미지를 적용하여 적응형 이진화 결과는 어떻게 나타나는지, 기존의 이진 이미지와 어떤 차이가 있는지 살펴보겠습니다. 아래 그림의 왼쪽은 adaptiveMethod를 ADAPTIVE_THRESH_MEAN_C, 오른쪽 그림은 ADAPTIVE_THRESH_GAUSSIAN_C로 설정했을 때 적응형 이진화의 결과입니다. 기존 이진 이미지에서는 경계값에 따라 이미지의 왼쪽 부분이 모두 검정색으로 표현되거나, 아래 부분이 모두 흰색으로 표현되었습니다. 반면에, 적응형 이진화를 적용한 결과에서는 모두 검정 또는 흰색으로 표현된 부분없이 모든 칸의 숫자들을 육안으로 잘 확인할 수 있습니다.
# 평균 가중치 기반 적응형 이진화
mean_bin = cv2.adaptiveThreshold(sudoku, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 51, 0)
# 가우시안 가중치 기반 적응형 이진화
gaus_bin = cv2.adaptiveThreshold(sudoku, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 51, 0)
fig, subs = plt.subplots(ncols = 2, figsize = (10, 5), sharex = True, sharey = True)
subs[0].set_title('ADAPTIVE_THRESH_MEAN_C')
subs[0].imshow(mean_bin, cmap = 'gray')
subs[1].set_title('ADAPTIVE_THRESH_GAUSSIAN_C')
subs[1].imshow(gaus_bin, cmap = 'gray')
plt.show()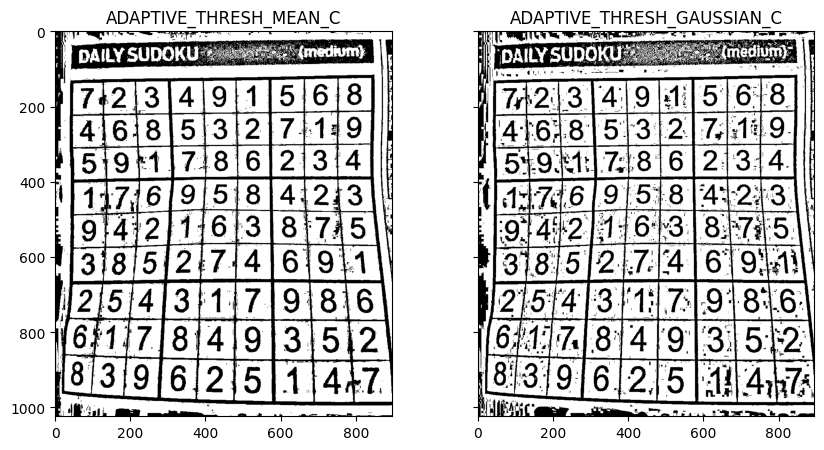
여기까지 OpenCV를 사용한 이미지 이진화 방법에 대해 알아봤습니다. 특정 경계값으로 이진화하는 cv2.threshold 보다도 주변 픽셀들을 사용해 경계값을 가변적으로 설정하는 적응형 이진화(cv2.adaptiveThreshold)를 활용했을 때 부분적인 명암에 관계없이 원하는 이진 이미지를 얻을 수 있다는 점도 예시를 통해 확인할 수 있었습니다.
다음 포스팅에서도 OpenCV를 활용한 이미지 처리 기법에 대해 다루겠습니다. 이상입니다.
감사합니다 :>
'인공지능 > 컴퓨터 비전' 카테고리의 다른 글
| 형상 분석과 측정 (feat. 형상 지표 종류) (0) | 2023.11.21 |
|---|---|
| Fully Convolutional Networks (FCN) (0) | 2023.01.11 |
| 합성곱 신경망 (Convolutional Neural Networks ; CNN) (0) | 2022.11.29 |
| OpenCV를 사용한 이미지 처리 - 블러링 (cv2.blur, cv2.GaussianBlur) (0) | 2022.11.21 |
| OpenCV를 사용한 이미지 처리 (설치, 읽기, 시각화) (2) | 2022.11.19 |
