※ 출처
* Michael A. Wirth, 2004. Shape Analysis & Measurement.
형상 분석과 측정
* 형상 측정의 목표
- 개체의 형상을 특징짓는 물리적 치수 측정 (형상의 정량화/특성화)
- 개체를 명확하게 구분하는 데에 필요한 최소한의 형상 특징을 측정
* 형상 측정의 성능
- 원본 이미지의 품질과 적절한 전처리 과정과 관련
. 원본 이미지의 품질 저하 : 이미지의 노이즈로 인해 형상 측정 결과가 좋지 않을 수 있음
* 형상 정보의 특징
. 형상 정보는 개체의 위치, 방향, 크기를 추출한 후에도 유지되는 정보
※ 자주 쓰이는 용어
* 경계 박스(Bounding Box)
- 개체를 둘러싸는 직사각형

* 볼록 껍질(Convex Hull)
- 개체를 포함하는 가장 작은 볼록 도형

거리(Distance) 관련 형상 지표
* 유클리드(Euclidean) 거리
d=√(x1−x2)2+(y1−y2)2
* 체비쇼프(Chebyshev) 또는 체스판(Chessboard) 거리
d=max
* 맨해튼(Manhattan) 또는 도시블록(City-block) 거리
d=\left| x_1 - x_2 \right| + \left| y_1 - y_2 \right|

면적(Area) 관련 형상 지표
* 면적 : 개체를 구성하는 픽셀 개수
* 볼록(Convex) 면적 : 개체를 둘러싸는 볼록 껍질의 면적

축(Axis) 관련 형상 지표
* 장축(Major Axis)
- 개체를 통해 그릴 수 있는 가장 긴 선의 (x, y) 끝점
- 연산 방법 : 개체 경계의 모든 픽셀들 간 조합에 대해 거리를 계산하고, 최대 길이를 갖는 두 픽셀 (x_1, y_1)과 (x_2,y_2)를 탐색
* 단축(Minor Axis)
- 장축과 수직이면서, 개체를 통해 그릴 수 있는 가장 짧은 선의 (x, y) 끝점

길이(Length) 관련 형상 지표
* 둘레(Perimeter) : 개체의 경계를 구성하는 픽셀 개수
\text{Perimeter}=\sum_{i=1}^{N-1} \left| x_i - x_{i+1} \right| (x \text{ in boundary})
* 볼록(Convex) 둘레 : 개체를 둘러싸는 볼록 껍질의 둘레

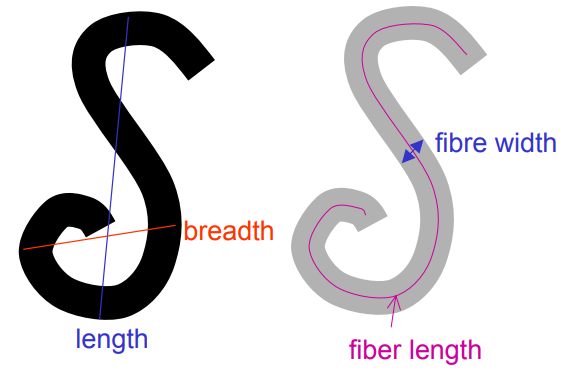
* 장축(Major Axis) 길이 또는 개체 길이(Length) : 장축 끝점 사이의 픽셀 거리
* 단축(Minor Axis) 길이 또는 개체 너비(Width) : 단축 끝점 사이의 픽셀 거리
* Fiber 길이
\text{Fiber Length} = { {\text{Perimeter}-\sqrt{{{\text{Perimeter}}^2} - 16\cdot\text{Area}}} \over {4} }
각도(Angle) 관련 형상 지표
* 장축(Major Axis) 각도 또는 개체 방향(Orientation)
- 개체의 장축과 X축 사이의 각도(0~360도)
- 형상의 전체적인 방향
\text{Major Axis Angle}=\arctan \left( {y_2 - y_1}\over {x_2 - x_1} \right)
Compactness
* 개체와 동일한 둘레를 갖는 원의 면적에 대한 개체 면적의 비율(0~1 사이의 값)
- 원은 가장 compact 한 형상을 가진 도형이므로 Compactness 값이 1
- 복잡하고 불규칙한 경계를 가진 개체일수록 Compactness 값이 감소
\text{Compactness}= {{4\pi\cdot\text{Area}}\over{\text{Perimeter}^2}}

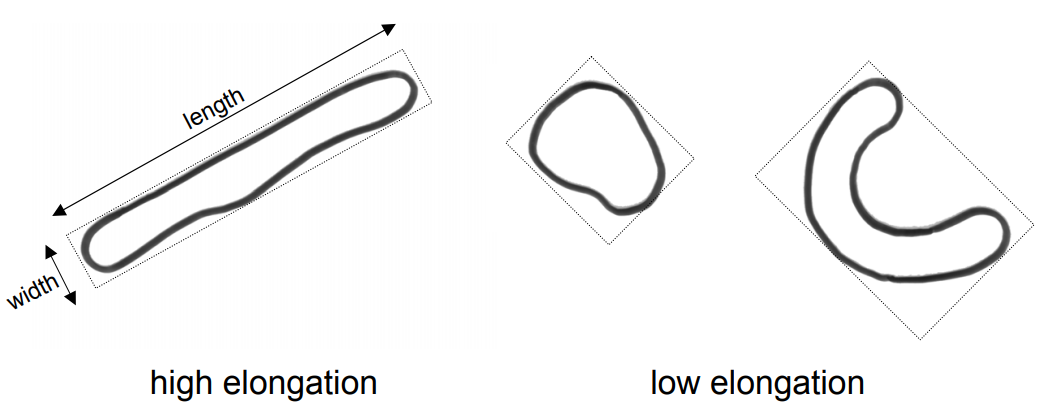
신장률(Elongation)
* 개체 경계 상자(bounding box)의 길이와 너비 간 비율(0~1 사이의 값)
- 신장률이 1이면 개체의 형상은 대략적으로 정사각형 또는 원형에 가까움
- 개체가 길어질수록 신장률이 1보다 커짐
\text{Elongation}= { {\text{Length}_{\text{Bounding Box}}} \over {\text{Width}_{\text{Bounding Box}}} }
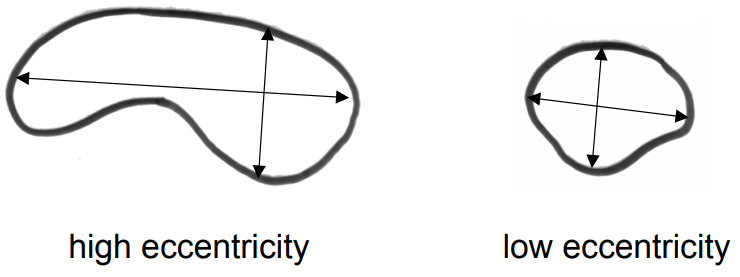
이심률(Eccentricity)
* 개체의 단축 길이에 대한 장축 길이의 비율
Eccentricity= { {\text{Major Axis Length}} \over {\text{Minor Axis Length}} }
원형도(Circularity or Roundness)
* 개체와 동일한 볼록 둘레를 갖는 원의 면적에 대한 개체 면적의 비율
- 원의 경우 원형도는 1, 원형과 멀어질수록 1보다 작아짐
- 단, 불규칙한 경계에 상대적으로 둔감함
\text{Circularity or Roundness}= { {4\pi\cdot\text{Area}} \over {\text{Convex Perimeter}^2} }

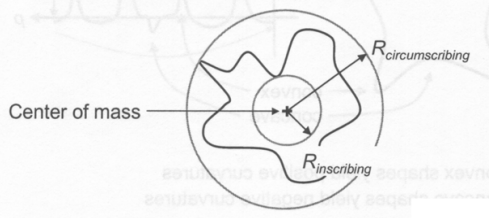
구형도(Sphericity)
* 개체가 구 모양에 가까운 정도
- 원의 경우 구형도는 최대값인 1
\text{Sphericity} = { {R_{\text{Inscribing}}} \over {R_{\text{circumscribing}}} }
볼록도(Convexity)
* 개체가 볼록한 개체와 얼마나 다른지 나타내는 상대적인 비율
- 개체 둘레에 대한 개체의 볼록 껍질 둘레의 비율
- 볼록한 개체는 1, 불규칙한 경계를 가진 개체는 1보다 작은 볼록도를 가짐
\text{Convexity}={ {\text{Convex Perimeter}} \over {\text{Perimeter}} }

종횡비(Aspect Ratio)
* 개체 높이와 너비의 비율
\text{Aspect Ratio} = { {\text{Height}} \over {\text{Width}} }
Curl
* 개체가 말려있는 정도
- 개체가 말려있을수록 Curl 값이 감소
\text{Curl} = { {\text{Length}} \over {\text{Fiber Length}} }
견고성(Solidity)
* 개체의 밀도를 나타냄
- 개체의 볼록 껍질 면적에 대한 개체 면적의 비율
- 견고성이 1보다 작으면 경계가 불규칙하거나 구멍이 있는 개체
\text{Solidity} = { {\text{Area}} \over {\text{Convex Area}} }

'인공지능 > 컴퓨터 비전' 카테고리의 다른 글
| OpenCV를 사용한 이미지 이진화 (cv2.threshold, cv2.adaptiveThreshold) (0) | 2023.02.14 |
|---|---|
| Fully Convolutional Networks (FCN) (0) | 2023.01.11 |
| 합성곱 신경망 (Convolutional Neural Networks ; CNN) (0) | 2022.11.29 |
| OpenCV를 사용한 이미지 처리 - 블러링 (cv2.blur, cv2.GaussianBlur) (0) | 2022.11.21 |
| OpenCV를 사용한 이미지 처리 (설치, 읽기, 시각화) (2) | 2022.11.19 |
